
Si possono però approssimare con tecniche di vario genere. La più semplice è quella di usare un polinomio, la più semplice funzione algebrica, nel senso che si può sempre calcolare.
Occorre definire le condizioni alle quali deve soddisfare un polinomio per essere considerato una "buona" approssimazione della funzione trascendente.
Una soluzione molto semplice è data dal polinomio di Maclaurin.
Il polinomio di McLaurin di grado n di una certa funzione $f(x)$ è quello che ha lo stesso valore della funzione per x = 0 e inoltre la stessa derivata prima per $x = 0$, la stessa derivata seconda e così via fino alla derivata ennesima.
In questo modo si impongono n+1 condizioni per n+1 incognite (i coefficienti del polinomio) il che vuol dire che avremo un sistema lineare e la soluzione sarà unica!
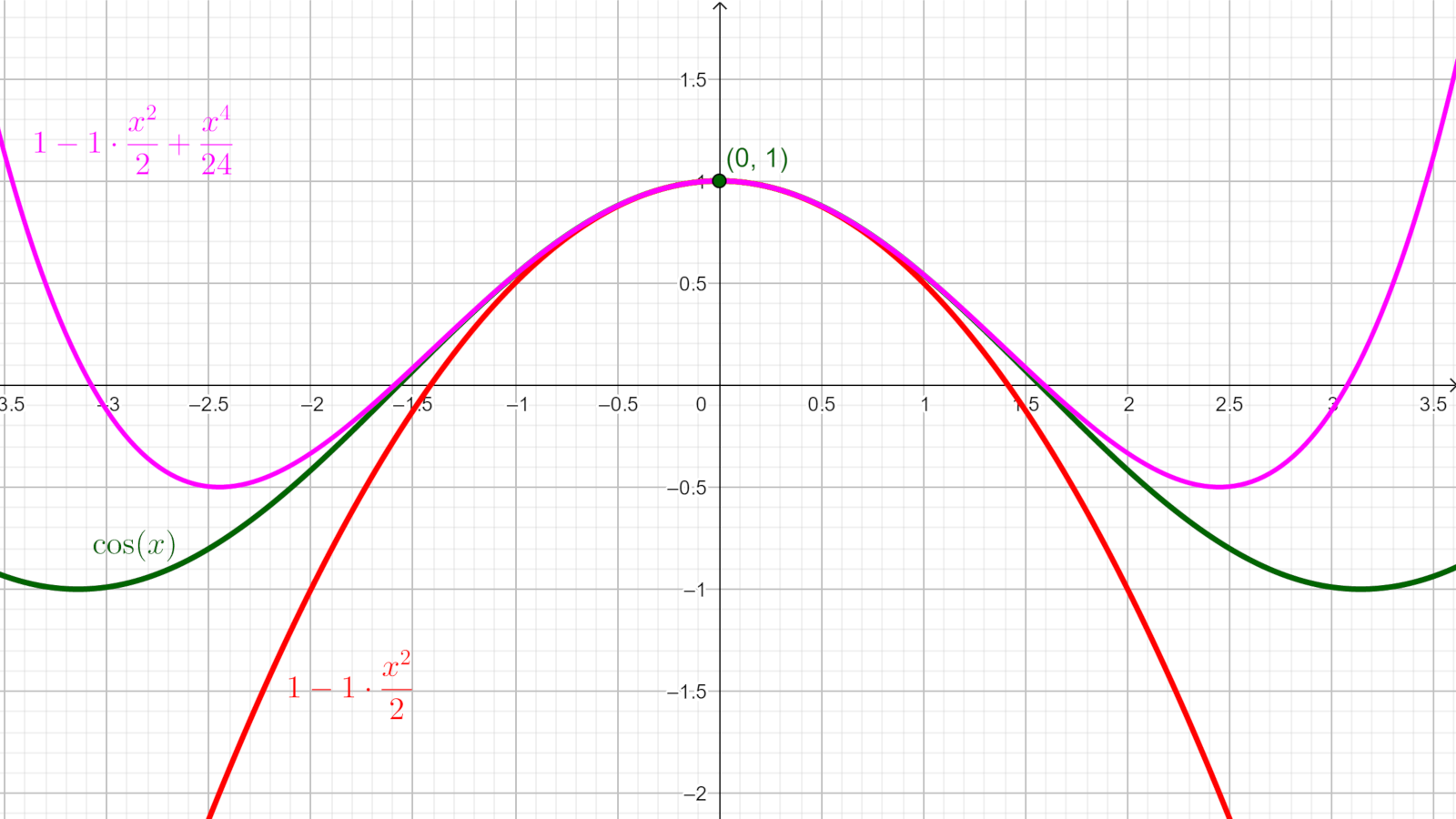
Per esempio proviamo a trovare il polinomio di Maclaurin di grado 2 che meglio approssima la funzione coseno, $f(x) = cos(x)$ le cui derivate sono:
$$ f'(x) = -sin(x) \\ f"(x) = -cos(x) $$Il polinomio di secondo grado sarà $P(x) = a + bx + cx^2$;
Le sue derivate rispetto alla $x$ sono
$$ P'(x) = b + 2cx \\ P"(x) = 2c $$Imponiamo ora che funzione e derivate coincidano per $x=0$; si ricava con facili passaggi:
$$ \begin{array}[l c l c l] \\ f(x) = cos(x) & & P(x) = a + bx + cx^2& & \cos(0) = a & & 1 = a & & a = 1 \\ f'(x) = -sin(x) & & P'(x) = b + 2cx & &\rightarrow & -\sin(0) = b & \rightarrow & 0 = b & \rightarrow & b = 0 \\ f"(x) = -cos(x) & & P"(x) = 2c & & -\cos(0) = 2c & & -1 = 2c & & c = -\frac{1}{2} \end{array} $$In definitiva il polinomio di Maclaurin di 2° grado che meglio approssima il coseno è:
$$ y = 1 - \frac{1}{2}x^2 $$Per ottenere il termine successivo basta aggiungere due linee per derivata terza e quarta con $P(x) = a + bx + cx^2 +dx^3 +e x^4$:
$$ \begin{array}[l c l c l] \\ f^{iii}(x) = sin(x) & & P^{iii}(x) = ... + 6d + 24ex & & \sin(0)= 0 & & 0 = 6d & \rightarrow & d = 0 \\ f^{iv}(x) = cos(x) & & P^{iv}(x) = ... 24e & & \cos(0) = 1 & & 4! e = 1 & & e = \frac{1}{4!} \end{array} $$ $$ y = 1 - \frac{1}{2}x^2 + \frac{1}{4!}x^4$$In generale il polinomio di Maclaurin di grado $2n$ per il coseno vale:
$$ P(x) = 1 - \frac{1}{2}x^2 + \frac{1}{4!}x^4 - \frac{1}{6!}x^6 .... + (-1)^n \frac{1}{(2n)!}x^{2n} + ...$$dove l'espressione (-1)^n indica semplicemente l'alternarsi dei segni.
Su altra pagina si dimostra la forma generale del polinomio di MacLaurin.
Tanto maggiore $n$, tanto migliore l'approssimazione! Si dimostra anzi che per $n$ tendente a infinito, la formula è esatta, in un certo senso quindi il coseno può vedersi come polinomio con infiniti termini.
Si noti infine che essendo il coseno una funzione pari, il polinomio di Maclaurin contiene solo termini di grado pari.
N.B. Il polinomio, come sempre in Analisi, va calcolato in radianti non in gradi!
Se invece che $x=0$ si usa un altro valore di $x$ si hanno i cosiddetti polinomi di Taylor. In realtà per funzioni periodiche come seno e coseno, è sufficiente saperle calcolare nell'intervallo $[0,45°] = [0, \frac{\pi}{4}]$; per un valore $x$ fuori di questo intervallo, basterà usare le opportune identità goniometriche per ridurlo al primo ottante cioè appunto l'intervallo suddetto.
L'approssimazione con Taylor e Mclaurin ha il difetto di non essere uniforme; molto buona nelle vicinanze di $x_0$ peggiora all'allontanarsi da questo valore. Si sono allora cercati polinomi che diano un'approssimazione con precisione uniforme in un dato intervallo, i più noti essendo i polinomi di Cebicef.