Tutti i metodi numerici per la ricerca degli zeri di una funzione $f(x)$ (ovvero le soluzioni o radici dell'equazione $f(x) = 0$) richiedono prima di tutto un algoritmo per cercare gli intervalli nei quali si trova un solo zero; questa operazione è detta di separazione delle radici.

Un primo metodo consiste nello studiare la funzione f(x), disegnare il grafico, e osservando il grafico ricavare gli intervalli in cui cadono gli zeri.

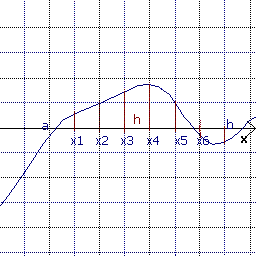
Un metodo più adatto alla realizzazione sul computer è quello della ricerca del cambiamento di segno; si calcola la funzione in un dato intervallo [a, b] cominciando da $a$ e con un passo $h$ si percorre tutto l'intervallo calcolando per ogni $x$ il corrispondente $y = f(x)$; quando si verifica un cambiamento di segno della y, si può concludere che c'è almeno uno zero in [x - h, x], alla condizione che la funzione sia continua nell'intervallo (questo risultato si basa sul teorema di Bolzano).

Si può allora procedere all'approssimazione dello zero con un metodo iterativo, come il metodo della bisezione, quello delle corde o quello delle tangenti.