

| La bisezione |
|---|
|
Un metodo molto semplice per approssimare le soluzioni di un'equazione $f(x) = 0$ (o che è lo stesso di calcolare gli zeri della funzione $y = f(x)$ in un intervallo [a, b]) è quello della bisezione.
Prima di tutto è necessario separare le soluzioni e cioè individuare un intervallo $[x_1, x_2]$ nel quale vi sia almeno una soluzione, e cioé un intervallo nel quale ci sia un cambiamento di segno della funzione.
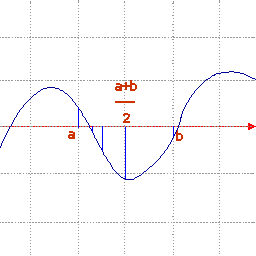
Nel disegno accanto la funzione $y=f(x)$ attraversa l'asse delle $x$ tra $x_1$ e $x_2$. Dunque vi è una soluzione tra $x_1$ e $x_2$.
Per restringere il campo la cosa più semplice è quella di dividere in due l'intervallo, calcolando la funzione nel suo punto medio. Dopo di chè si individua in quale delle due metà si verifica ancora un cambiamento di segno: la soluzione si trova di certo in questo nuovo intervallo dimezzato. Il procedimento può ora ripetersi quante volte si vuole fino a ottenere la precisione voluta.
In pratica date $x_1$ e $x_2$, si calcola il valore medio:
$$ x = \frac{x_1 + x_2}{2} $$ e quindi $y = f(x)$Il metodo della bisezione ha una convergenza piuttosto lenta; una maggiore velocità si può ottenere con due metodi classici: quello della secante (o regula falsi) e quello della tangente (o di Newton).
Questo algoritmo può facilmente realizzarsi con un qualsiasi linguaggio di programmazione, p.es. C, Pascal. Qui presentiamo una versione PhP.