

| caso 1 caso 2 caso 3 caso 4 |
|
Questo metodo permette di approssimare le soluzioni di un'equazione f(x) = 0 (o che è lo stesso di calcolare gli zeri della funzione y = f(x) in un intervallo [a, b] alla sola condizione di saper calcolare la funzione e la sua derivata in tutto l'intervallo.
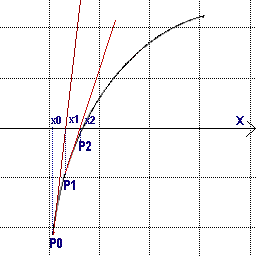
Prima di tutto è necessario separare le soluzioni e cioè individuare gli intervalli nei quali cadono le singole soluzioni. In questo caso è necessario individuare un punto di innesco P0(x0;y0) che sia abbastanza vicino a una soluzione, nel senso che la concavità non cambi di segno nell'intervallo.
Nel disegno accanto la funzione y=f(x) attraversa l'asse delle x vicino ad x0. Del punto P0 dobbiamo essere in grado di calcolare il valore della funzione f(x0) e della derivata f'(x0)
Dal punto P0 si può ora tracciare la tangente alla curva; tale tangente incontrerà l'asse delle ascisse per un valore di x che è la prima approssimazione della soluzione cercata.
La tangente avrà per coefficiente angolare il valore della derivata in P0, f'(x0). Utilizzando l'equazione della retta generica (o fascio di rette) per P0: y-y0 = m(x-x0), sostituendo m con f'(x0) e imponendo y = 0 si ha:
−y0 = f'(x0)(x−x0)
A questo punto si risolve rispetto alla x e si ha con facili passaggi:
y0
x = x0 − ————————
f'(x0)
o anche ricordando che y0 = f(x0)
f(x0)
x = x0 − ————————
f'(x0)
Il procedimento si può iterare, calcolando il valore y = f(x), tracciando la tangente per questo nuovo punto ecc.ecc. In generale, chiamando xn l'ennesima approssimazione e xn+1 quella successiva si ha la classica formula di Newton:
f(xn)
xn+1 = xn − ———————
f'(xn)
Il procedimento è convergente, nel senso che fissato un margine di errore piccolo quanto si vuole, si troverà sempre una approssimazione per la quale l'errore è minore di tale margine.
Il metodo si traduce facilmente in un algoritmo in un qualsiasi linguaggio di programmazione; si veda p.es. l'algoritmo in PhP.