

Come il seno anche il coseno è una funzione trascendente che può calcolarsi solo in alcuni casi fortunati: per $x = 0; x = \frac{\pi}{6} x = \frac{\pi}{4}$ ecc.ecc.
il polinomio di Maclaurin fornisce uno strumento per approssimare il coseno di x nelle vicinanze di $x = 0$.
Nel caso della $f(x) = cos(x)$ le prime quattro derivate successive sono:
| $f(x) = cos(x)$ | $f(0) = 1$ | $P(x) = a_0 + a_1.x + a_2.x^2 + a_3.x^3 + a_4.x^4$ | $P(0) = a_0$ |
| $f'(x) = -sin(x)$ | $f'(0) = 0$ | $P'(x) = a_1 + 2a_2.x + 3a_3.x^2 + 4a_4.x^3$ | $P'(0) = a_1$ |
| $f"(x) = -cos(x)$ | $f"(0) = -1$ | $P"(x) = 2.a_2 + 6a_3.x + 12a_4.x^2$ | $P"(0) = 2.a_2$ |
| $f^{iii}(x) = sin(x)$ | $f^{iii}(0) = 0$ | $P^{iii}(x)= 6.a_3 + 24.a_4.x$ | $P^{iii}(0) = 6.a_3$ |
| $f^{iv}(x) = cos(x)$ | $f^{iv}(0) = 1$ | $P^{iv}(x)= 24a_4 = 4!.a_4$ | $P^{iv}(0) = 24.a_4$ |
Poichè sin(0) = 0 tutti i termini di ordine dispari scompaiono, e restano solo quelli di ordine pari come è logico essendo appunto il coseno una funzione pari. Lo specchietto sottostante mostra come si arriva al polinomio di Maclaurin di grado 4.
| a_0 = 1 | a_1 = 0 | a_2 = -1/2 | a_3 = 0 | a_4 = 1/24 |
| P(x) = 1 - x^2/2 + x^4/24 | ||||
Più in generale il polinomio è:
$$P(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \frac{x^8}{8!} ...$$
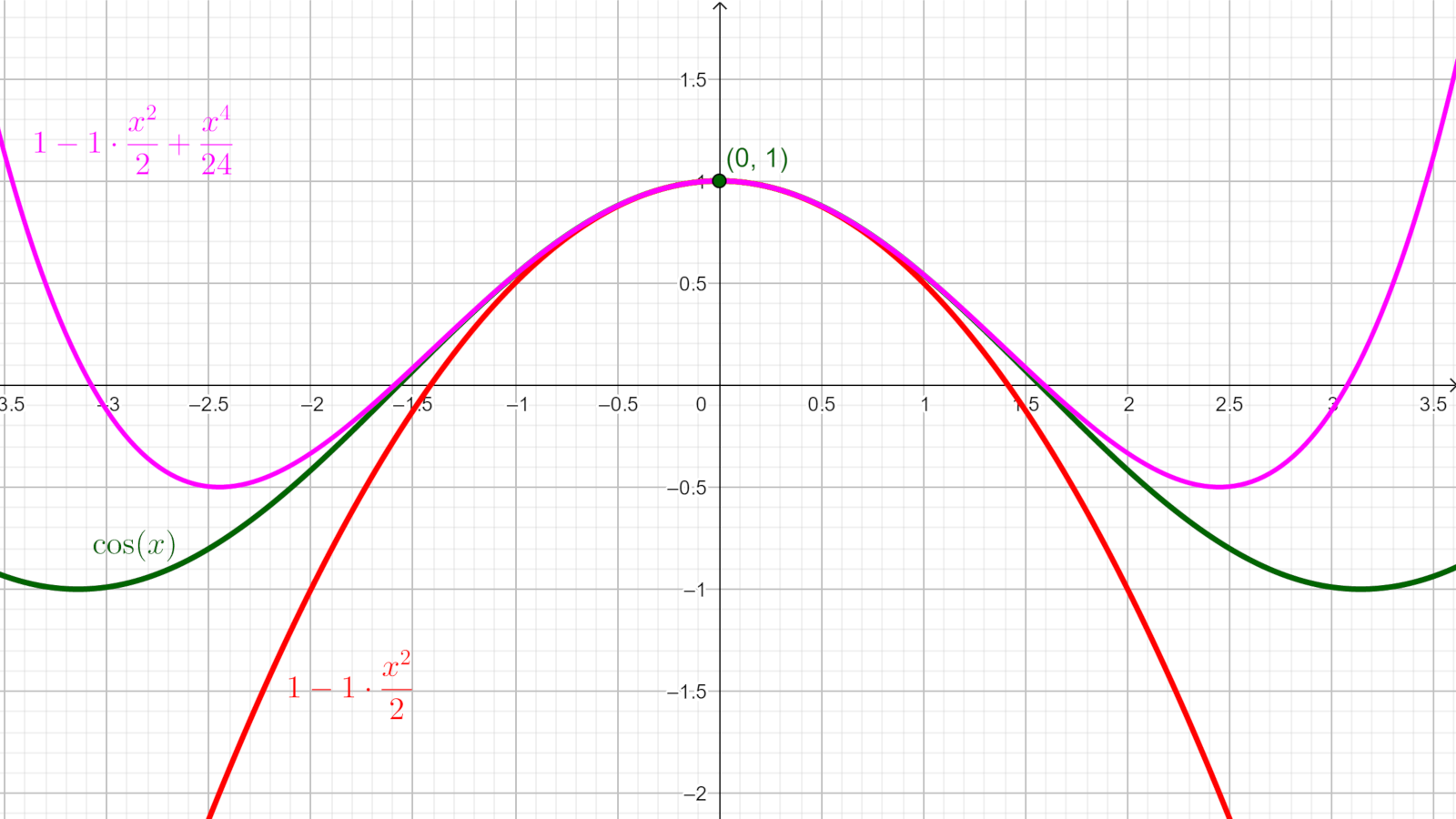
Nel disegno sono riportati i grafici del cosinusoide y = cos(x) (la $x$, come sempre in Analisi, deve essere in radianti) e quelli dei primi polinomi di Maclaurin; quello di grado 1 si riduce alla retta $y = 1$, che è poi la tangente al cosinusoide; quello di grado $2$ è la parabola $y = 1 - \frac{x^2}{2!}$.
Si osservi come al crescere del grado aumenti la precisione dell'approssimazione, che resta comunque buona solo nelle vicinanze dell'origine; d'altra parte essendo il coseno una funzione periodica è sufficiente approssimarla tra 0 e $\frac{\pi}{4}$ alias $45^{o}$, per essere in grado di approssimarla per qualsiasi valore. Quindi si deve scegliere un numero di iterazione che dia per $\frac{\pi}{4}$ un errore minore del desiderato, per averlo per qualsiasi valore della $x$.
Sono state trovare diverse formule per stimare l'errore, in analisi chiamato il resto.