

| caso 1 caso 2 caso 3 caso 4 |
|
Questo metodo permette di approssimare le soluzioni di un'equazione $f(x) = 0$ (o che è lo stesso di calcolare gli zeri della funzione $y = f(x)$ in un intervallo [a, b] alla condizione di saper calcolare la funzione in tutto l'intervallo.
Prima di tutto è necessario separare le soluzioni e cioè individuare gli intervalli nei quali cadono le singole soluzioni. Una volta individuato un intervallo $[x_0, x_1]$ nel quale cade una soluzione si può passare all'approssimazione della soluzione.
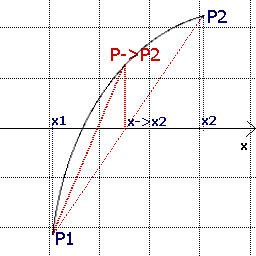
Nel disegno accanto la funzione $y=f(x)$ attraversa l'asse delle $x$ tra $x_0$ e $x_0$. Dei due punti $P_0$ e $P_1$ possiamo calcolare le ordinate $y = f(x)$.
Viene allora naturale l'idea di tracciare il segmento di retta $P_0 P_1$ (ovvero la $corda$ o $secante$) che unisce i due punti; tale segmento incontrerà l'asse delle $x$ per un'ascissa che possiamo prendere come prima approssimazione della soluzione cercata.
questa approssimazione si può calcolare facilmente determinando l'equazione della retta per due punti e quindi calcolando l'intersezione tra questa retta e l'asse delle $x$. Si può anzi ricavare la seguente formula iterativa che fornisce l'approssimazione $x$ in funzione delle coordinate dei due punti:
$$x = x_0 - y_0\frac{x_1 - x_0}{y_1 - y_0}$$Una volta calcolata questa approssimazione $x$, il procedimento si può iterare, calcolando il valore della $y = f(x)$, sostituendo questo punto a uno dei due precedenti, a seconda dei quattro casi possibili, conducendo una nuova secante, calcolando una seconda approssimazione e così via.
Ripeti
x ← x0 - y0*(x1-x0)/(y1-y0);
y ← f(x);
se (y y1 hanno lo stesso segno){
x1 ← x; y1 ← y;
altrimenti
x0 ← x; y0 ← y;
Finché la differenza (x1-x0) non è minore della precisione desiderata
L'algoritmo è convergente, nel senso che fissato un margine di errore piccolo quanto si vuole, si troverà sempre una approssimazione per la quale l'errore è minore di tale margine. Ne segue che in teoria l'algoritmo precedente si fermerà sempre quale che sia la precisione desiderata. Nel mondo reale però i numeri possono rappresentarsi solo con un numero finito di cifre, e quindi se si richiede una precisione troppo piccola può accadere che l'algoritmo possa andare in loop infinito se per errori di arrotondamento la differenza tra i due numeri $x_1$ e $x_0$ non arrivi mai a zero. Per essere assolutamente sicuri a volte si sostituisce la logica del "ripeti" in un "ripeti n volte" con $n$ stimato a priori come un numero di iterazioni sufficienti a dare la precisione desiderata.
Detto questo, l'algoritmo si implementa facilmente in un qualsiasi linguaggio di programmazione; si veda p.es. quello in Php.